Расчет площади воздуховодов
Прямой участок воздуховода
| Площадь воздуховода круглого сечения | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|||||||||
|
|
|||||||||
| Площадь воздуховода прямоугольного сечения | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||
|
Площадь 0 м |
|||||||||||||
Отводы
| Площадь отвода круглого сечения | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|||||||||
| Площадь 0 м2 | |||||||||
| Площадь отвода прямоугольного сечения | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||
| Площадь 0 м2 | |||||||||||||
Переходы
| Площадь перехода круглого сечения | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||
| Площадь 0 м2 | |||||||||||||
| Площадь перехода прямоугольного сечения | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||
| Площадь 0 м2 | |||||||||||||||||
| Площадь перехода с прямоугольного сечения на прямоугольное | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||||
| Площадь 0 м2 | |||||||||||||||||||||
Тройники
| Площадь тройника круглого сечения | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||
| Площадь 0 м2 | |||||||||||||||||
| Площадь тройника круглого сечения | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||||
| Площадь 0 м2 | |||||||||||||||||||||
| Площадь тройника прямоугольного сечения | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||||
| Площадь 0 м2 | |||||||||||||||||||||
| Площадь тройника прямоугольного сечения | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||||||||
| Площадь 0 м2 | |||||||||||||||||||||||||
Заглушки
| Площадь заглушки круглого сечения | |||||
|---|---|---|---|---|---|
|
|||||
| Площадь 0 м2 | |||||
| Площадь заглушки прямоугольного сечения | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|||||||||
| Площадь 0 м2 | |||||||||
Утка прямоугольного сечения
| Площадь утки со смещением в 1-ой плоскости | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||
| Площадь 0 м2 | |||||||||||||||||
| Площадь утки со смещением в 2-х плоскостях | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||||
| Площадь 0 м2 | |||||||||||||||||||||
Зонты
| Площадь зонта островного типа | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||||
| Площадь 0 м2 | |||||||||||||||||||||
| Площадь зонта пристенного типа | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||
| Площадь 0 м2 | |||||||||||||||||
Врезки
| Площадь врезки прямой круглой | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|||||||||
| Площадь 0 м2 | |||||||||
| Площадь врезки прямой прямоугольной | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||
| Площадь 0 м2 | |||||||||||||
| Площадь круглой врезки с воротником | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||
| Площадь 0 м2 | |||||||||||||
| Площадь прямоугольной врезки с воротником | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||
| Площадь 0 м2 | |||||||||||||||||
Расчет системы вентиляции, онлайн калькулятор
Онлайн-калькулятор расчета производительности вентиляции
Расчет вентиляции, как правило, начинается с подбора оборудования, подходящего по таким параметрам, как производительность по прокачиваемому объему воздуха и измеряемому в кубометрах в час. Важным показателем в системе является кратность воздухообмена. Кратность воздухообмена показывает, сколько раз происходит полная замена воздуха в помещении в течение часа. Кратность воздухообмена определяется СНиП и зависит от:
- назначения помещения
- количества оборудования
- выделяющего тепло,
- количества людей в помещении.
В сумме все значения по кратности воздухообмена для всех помещений составляют производительность по воздуху.
Расчет производительности по кратности воздухообмена
Онлайн-калькулятор расчета системы вентиляцииСледующий этап в расчете вентиляции — проектирование воздухораспределительной сети, состоящей из следующих компонентов: воздуховоды, распределители воздуха, фасонные изделия (переходники, повороты, разветвители.) Сначала разрабатывается схема воздуховодов вентиляции, по которой производится расчет уровня шума, напора по сети и скорости потока воздуха. Напор по сети напрямую зависит от того, какова мощность используемого вентилятора и рассчитывается с учетом диаметров воздуховодов, количества переходов с одного диаметра на другой, и количества поворотов. Напор по сети должен возрастать с увеличением длины воздуховодов и количества поворотов и переходов. Расчет количества диффузоров
| ||||||||||||||||
Проектируя системы вентиляции, необходимо находить оптимальное соотношение между мощностью вентилятора, уровнем шума и диаметром воздуховодов. Расчет мощности калорифера производится с учетом необходимой температуры в помещении и нижним уровнем температуры воздуха снаружи.
Расчет мощности калорифера
| Методика расчета мощности калорифера Р = T * L * Сv / 1000, где: Р — мощность прибора, кВт; |
Также при выборе оборудования для системы вентиляции необходимо рассчитать следующие параметры:
- Производительность по воздуху;
- Мощность калорифера;
- Рабочее давление, создаваемое вентилятором;
- Скорость потока воздуха и площадь сечения воздуховодов;
- Допустимый уровень шума.
Калькуляторы для расчета площади — ООО ГОТИКА
Калькулятор для расчета мощности кондиционера
Cторона освещения помещенияСеверЮго-запад, юго-востокЮг
Необходимая мощность кондиционера (BTU) =
1150
Необходимая мощность кондиционера (кВт) =
1.15
Расчет площади поверхности трубы позволяет быстро определить объем работ и расчетное количество материалов.
Площадь воздуховода круглого сечения

Площадь воздуховода прямоугольного сечения

Площадь отвода круглого сечения

1530456090
Площадь отвода прямоугольного сечения

1530456090
Площадь перехода круглого сечения

Площадь перехода прямоугольного сечения

Площадь перехода с прямоугольного сечения на прямоугольное

Площадь тройника круглого сечения

Площадь тройника круглого сечения

Площадь тройника прямоугольного сечения (на круг)

Площадь тройника прямоугольного сечения (на квадрат)

Площадь заглушки круглого сечения

Площадь заглушки прямоугольного сечения

Утка прямоугольного сечения
Площадь утки со смещением в 1-ой плоскости

Площадь утки со смещением в 2-х плоскостях

Площадь зонта островного типа

Площадь зонта пристенного типа

Зонты и дефлекторы
Площадь круглого зонта

Площадь дефлектора

Площадь квадратного зонта

Площадь прямоугольного зонта

Расчет площади воздуховодов — онлайн калькулятор
Автор Евгений Апрелев На чтение 3 мин. Просмотров 9.1k.
Вентиляция играет важнейшую роль в создании оптимального микроклимата в жилище. Правильно сконструированная вентиляционная система обеспечивает вывод за пределы помещения загрязненного воздуха, вредных газов, паров и пыли, которые влияют на здоровье людей, находящихся в жилом помещении. При проектировании вентиляционных систем производится огромное количество расчетов, в которых учитывается множество факторов и переменных.
В производительности вентиляционной системы не последнюю роль играю воздуховоды, а именно их длина, сечение и форма. Крайне важно чтобы расчет сечения воздуховодов был произведен правильно, так как именно от этого будет зависеть, сможет ли система воздуховодов пропускать достаточное количество воздуха, скорость воздушного потока и бесперебойная работа вентиляционной системы в целом. Благодаря грамотному расчету площади воздушных каналов, вибрация и аэродинамические шумы, производимые воздушными потоками, будут находиться в пределах допустимой нормы.
Рассчитать площадь воздуховодов для естественной вентиляционной системы можно тремя способами:
- Обратиться к профессионалам. Расчет будет произведен качественно, но дорого.
- Сделать самостоятельный расчет, используя формулы расчета удельных потерь воздуха, гравитационного подпора, поперечного сечения воздуховодов, формулу скорости движения воздушных масс в газоходах, определение потерь на трение и сопротивление.
- Воспользоваться онлайн-калькулятором.
Расчет сечения воздуховода
Для того чтобы воспользоваться онлайн-калькулятором, не нужно иметь инженерного образования или платить денег, просто введите в каждое поле калькулятора необходимые данные и получите правильный результат.
Методика самостоятельного расчета сечения воздуховодов
- Определение аэродинамических характеристик воздушного канала с естественным движением воздуха.
Rуд = Pгр/ ∑L
где
Pгр – гравитационное давление в каналах вытяжной вентиляции, Па;
L – расчетная длина участка, м.
При естественном побуждении необходимо увязать показатели гравитационных давлений в проходных каналах помещений с показателями трения и местными сопротивлениями, которые возникают по пути движения воздуха от вытяжки до устья вытяжной шахты, а именно по равенству 1, где ∑(Rln+Z) – расчетное снижение давления на местные сопротивления и трение на отрезках воздуховодов в расчетном направлении движения воздушных масс.
- Определение значения гравитационного подпора
Pгр= h(pn—pb)9.81
где
h – высота столба воздуха, м;
pn – плотность воздушных масс снаружи помещения, кг/м3,
pb – плотность воздушных масс в помещении.
- Площадь сечения воздуховода определяется по формуле
S = L * 2.778/V
где
S – расчетная площадь сечения воздуховода см2
L – расход воздуха через воздуховод, м3/час
V – скорость движения воздуха в воздуховоде, м/с,
2,788 – коэффициент для согласования размерностей.
- Фактическая площадь сечения воздуховодов определяется по формулам:
S = π * D / 400 – для круглых воздуховодов
S = A * B / 100 – для прямоугольных воздуховодов
где
S – фактическая площадь сечения, см2
D – диаметр круглого воздуховода, мм
A и B – ширина и высота прямоугольного воздуховода, мм.
- Для расчета сопротивления сети воздуховодов используется формула:
P = R * L + Ei * V2 * Y/2 где:
R – удельные потери на трение на конкретном участке вентиляционной сети
L – длина участка воздуховода.
Ei – сумма коэффициентов местных потерь на участке воздуховода
V2 – скорость движения воздуха на участке воздуховода
Y – плотность воздуха.
Скорость в воздуховоде

Скорость в воздуховоде — британские единицы
Скорость воздуха в вентиляционном канале может быть рассчитана в британских единицах как
v i = q i / A i
= q i / [ π (d f /2) 2 )]
= q i / [ π ((d i /12 ) / 2) 2 )]
= (576/ π) ( q i / d i 2 )
= 144 q i / (a i b i ) (1)
где
v i = скорость воздуха (фут / мин)
q i = расход воздуха (фут 3 / мин)
900 11 A i = площадь воздуховода (футы 2 )
d f = диаметр воздуховода (футы)
d i = диаметр воздуховода (дюймы)
a i = ширина воздуховода (дюймы)
b i = ширина воздуховода (дюймы)
Пример — скорость воздушного потока в воздуховоде
Скорость в 12-дюймовом воздуховоде с воздухом расход 1000 куб. футов в минуту можно рассчитать как
v i = (576/ π ) (1000 куб. футов в минуту) / (12 дюймов) 2 )
= 1273 (фут / мин)
Калькулятор скорости воздушного потока — британские единицы
Скорость воздуха можно рассчитать с помощью калькулятора, приведенного ниже.Добавьте объем воздуха — q — и диаметр — d — (или длину a и b ).
Связанные мобильные приложения из Engineering ToolBox 
— бесплатные приложения для автономного использования на мобильных устройствах
Скорость воздуха в воздуховоде — единицы СИ
Скорость воздуха в воздуховоде может быть рассчитана в единицах СИ
v м = q м / A м
= q м / (π (d м /2) 2 )
= 4 q м / (π d м 2 )
= q м / (a м b м ) (2)
где
v м = скорость воздуха (м / с )
q м = расход воздуха (м 3 / с)
A м = площадь воздуховода (м 2 )
d м = диаметр воздуховода (м)
a м = ширина воздуховода (м)
b м = ширина воздуховода (м)
Пример — скорость воздушного потока в воздуховоде
Скорость в прямоугольном 0.5 м x 0,5 м воздуховод с потоком воздуха 1 м 3 / с можно рассчитать как
v м = (1 м 3 / с) / ((0,5 м) (0,5 м))
= 4 (м / с)
Калькулятор скорости воздушного потока — единицы СИ
Скорость воздуха можно рассчитать с помощью калькулятора, приведенного ниже. Добавьте объем воздуха — q — и диаметр — d — (или длину a и b ).
Воздуховоды — Диаграмма скоростей
Приведенную ниже диаграмму можно использовать для оценки скоростей в воздуховодах.
Значения по умолчанию для воздушного потока 400 кубических футов в минуту (680 м 3 / ч) , размера воздуховода 8 дюймов (200 мм) и скорости 1150 футов в минуту (5,8 м / с) .

Загрузите и распечатайте воздуховоды — диаграмма скоростей!
Потери на трение в воздуховодах
Калькулятор площади
Ниже приведены калькуляторы для оценки площади семи распространенных форм. Площадь более сложных форм обычно можно получить, разбив их на совокупность простых форм и суммируя их площади. Этот калькулятор особенно полезен для оценки земельной площади.
Прямоугольник
Треугольник
Используйте калькулятор треугольника, чтобы определить |
Трапеция
Круг
Сектор
Эллипс
Параллелограмм
Калькулятор площади сопутствующих поверхностей | Калькулятор объема
Площадь — это величина, которая описывает размер или размер двухмерной фигуры или формы на плоскости.Его можно визуализировать как количество краски, которое потребуется для покрытия поверхности, и оно является двумерным эквивалентом одномерной длины кривой и трехмерного объема твердого тела. Стандартная единица площади в Международной системе единиц (СИ) — квадратный метр, или м 2 . Ниже приведены уравнения для некоторых наиболее распространенных простых форм и примеры того, как рассчитывается площадь каждой из них.
Прямоугольник
Прямоугольник — это четырехугольник с четырьмя прямыми углами.Это одна из простейших форм, и для расчета ее площади необходимо только знать (или измерить) ее длину и ширину. Четырехугольник по определению — это многоугольник, имеющий четыре ребра и вершины. В случае прямоугольника длина обычно относится к двум более длинным краям четырехугольника, а ширина относится к более коротким из двух краев. Когда длина и ширина прямоугольника равны, форма представляет собой особый случай прямоугольника, называемый квадратом. Уравнение для вычисления площади прямоугольника выглядит следующим образом:
площадь = длина × ширина
Фермер и его дочь — непроданная земля
Представьте, что фермер пытается продать участок земли совершенно прямоугольной формы.Поскольку у него есть несколько коров, которые он не хотел бы свободно резвиться, он огородил участок земли и знает точную длину и ширину каждого края. Фермер также живет в Соединенных Штатах и, не знаком с использованием единиц СИ, по-прежнему измеряет свой участок земли в футах. Стопа была определена как ровно 0,3048 метра в 1959 году после того, как она изменилась в течение длительного периода времени, поскольку исторически человеческое тело часто использовалось в качестве основы для единиц длины, и неудивительно, что она была непоследовательной в зависимости от времени и местоположения.В стороне, участок земли фермера имеет длину 220 футов и ширину 99 футов. Используя эту информацию:
площадь = 220 × 99 = 21780 кв. Футов
Земельный участок фермера, который имеет площадь 21 780 квадратных футов, равен половине акра, где акр определяется как площадь 1 цепи на 1 фарлонг, которые определяются чем-то другим, и так далее, и почему СИ сейчас существует. К несчастью для фермера, он живет в районе, где преобладают иностранные инвесторы с меньшим размером ноги, которые считали, что им следует получить больше квадратных футов за свои деньги, и его земля остается непроданной сегодня.
Треугольник
Существует множество уравнений для вычисления площади треугольника в зависимости от имеющейся информации. Как упоминалось в калькуляторе выше, используйте Калькулятор треугольников для получения дополнительных сведений и уравнений для расчета площади треугольника, а также для определения сторон треугольника с использованием любой доступной информации. Вкратце, уравнение, используемое в приведенном выше калькуляторе, известно как формула Герона (иногда называемая формулой Героя), относящаяся к герою Александрии, греческому математику и инженеру, которого некоторые считали величайшим экспериментатором древних времен.Формула выглядит следующим образом:
Фермер и его дочь — Triangle Daze
В этот момент, благодаря огромным усилиям и настойчивости, фермер, наконец, продал свой участок земли площадью 21 780 квадратных футов и решил использовать часть заработанных денег, чтобы построить бассейн для своей семьи. К несчастью для фермера, он не принимает во внимание тот факт, что одни только расходы на обслуживание бассейна в течение одного года, вероятно, могут покрыть посещение его детьми любого бассейна или аквапарка на долгие годы.Еще более печально для фермера, его 7-летняя дочь, которая недавно приехала в Египет через Дору-исследовательницу, влюбилась в треугольники и настаивает на том, чтобы бассейн был не только треугольной формы, но и необходимыми размерами. должна включать только цифру 7, чтобы обозначить ее возраст и увековечить этот момент ее жизни в форме треугольного бассейна. Как любящий отец, фермер соглашается на просьбу дочери и приступает к планированию строительства своего треугольного бассейна.Теперь фермер должен определить, достаточно ли у него на заднем дворе площади для размещения бассейна. В то время как фермер начал узнавать больше об единицах СИ, он все еще испытывает дискомфорт от их использования и решает, что его единственный жизнеспособный вариант — построить бассейн в форме равностороннего треугольника со сторонами 77 футов в длину, поскольку любой другой вариант будет либо слишком большим, либо маленьким. Учитывая эти размеры, фермер определяет необходимую площадь следующим образом:
Поскольку наибольшее расстояние между любыми двумя точками равностороннего треугольника — это длина ребра треугольника, фермер резервирует края бассейна для плавания «кругов» в своем треугольном бассейне с максимальной длиной примерно вдвое меньшей, чем у олимпийского. бассейн, но с двойной площадью — все под бдительным взором правящей королевы бассейна, его дочери и неодобрительного взгляда его жены.
Трапеция
Трапеция — это простой выпуклый четырехугольник, у которого есть по крайней мере одна пара параллельных сторон. Свойство быть выпуклым означает, что угол трапеции не превышает 180 ° (в отличие от вогнутого четырехугольника), в то время как простота отражает то, что трапеции не самопересекаются, то есть две несмежные стороны не пересекаются. В трапеции параллельные стороны называются основаниями трапеции, а две другие стороны называются ногами.Существует больше различий и классификаций для различных типов трапеций, но их площади по-прежнему рассчитываются таким же образом с использованием следующего уравнения:
где b 1 и b 2 — базы. h — высота, или перпендикулярное расстояние между основаниями
Фермер и его дочь — попытки разгрома
Прошло два года с тех пор, как бассейн фермера был достроен, а его дочь выросла и повзрослела.Хотя ее любовь к треугольникам все еще сохраняется, она в конце концов пришла к осознанию того, что независимо от того, насколько хорошо она была «треугольной», сами по себе треугольники не могут заставить мир вращаться, и что мастерская Санты не может правдоподобно балансировать на Северном полюсе, если бы мир скорее пирамида, чем сфера. Постепенно она начала принимать другие формы в своей жизни и преследовала множество различных интересов — в настоящее время — фристайл BMX. Таким образом, ей требуется пандус, но, к сожалению для фермера, не просто пандус.Пандус должен состоять только из форм, которые могут быть сформированы из нескольких треугольников, поскольку, как и ее рэп-идол Б.о.Б., дочери фермера все еще трудно принять реальность изогнутых поверхностей. Конечно, он должен использовать только цифру 9 в своих измерениях, чтобы отразить ее возраст. Фермер решает, что его лучший вариант — построить пандус, состоящий из нескольких прямоугольников, при этом боковая поверхность пандуса имеет форму трапеции. По мере того, как фермер теперь привык к SI, он может быть более креативным в использовании единиц и может построить рампу более разумного размера, придерживаясь требований своей дочери.Он решает построить пандус с трапециевидной поверхностью высотой 9 футов, нижним основанием длиной 29,528 футов (9 м) и верхним основанием 9 футов. Площадь трапеции рассчитывается следующим образом:
| площадь = | × 9 = 173,376 кв. Футов |
Круг
Круг — это простая замкнутая форма, образованная множеством всех точек на плоскости, находящихся на заданном расстоянии от заданной центральной точки. Это расстояние от центра до любой точки на окружности называется радиусом.Более подробную информацию о кругах можно найти на странице калькулятора круга, но для вычисления площади необходимо только знать радиус и понимать, что значения в круге связаны математической константой π . Уравнение для вычисления площади круга выглядит следующим образом:
площадь = πr 2
Фермер и его дочь — Круг Ли (ж)
Прошло еще шесть лет, и его дочь превратилась в сильного, красивого, влиятельного, уверенного в себе 15-летнего неблагодарного, сосредоточенного исключительно на поиске внешнего подтверждения со стороны знакомых и незнакомых людей в социальных сетях, при этом полностью игнорируя искреннюю поддержку со стороны ближайших родственников и друзей. .После спора со своим отцом по поводу чрезмерного использования социальных сетей, она решает использовать страх отца перед неизвестным и веру в сверхъестественное, чтобы разыграть его. Не зная, с чего начать, она ходит по городу, разговаривая с множеством незнакомцев, у каждого из которых, по-видимому, есть бесконечные источники мудрости и советов, где она узнает о кругах на полях и их связи с инопланетянами и неопознанными летающими объектами, а также на многие другие темы, которые игнорируйте все научные и логические объяснения.Убедившись, наконец, в сферической природе Земли, удалив все свои прошлые сообщения в социальных сетях, касающихся BoB, и расширив свою любовь к треугольникам до принятия других форм, она решает сделать основной круг на полях, состоящий из ряда концентрических кругов и хочет определить площадь, необходимую для создания кругов на полях с внешним радиусом 15 футов. Она делает это, используя следующее уравнение:
площадь = π × 15 2 = 706,858 кв. Футов
К несчастью для фермера, он не только напуган кругами на полях, которые появились ночью в ту ночь, когда его дочь сказала ему, что она была на вечеринке со своими друзьями, что по какой-то странной причине не привело к лишним постам в Instagram (он был, конечно, первым последователем своей дочери), но количество «исследователей круга» и «цереологов», появившихся на его ферме, чтобы изучить и впоследствии подтвердить подлинность кругов на полях как инопланетной конструкции, стоило ему значительного ущерба для его посевов .
Сектор
Сектор круга — это по существу часть круга, заключенного между двумя радиусами и дугой. Учитывая радиус и угол, площадь сектора можно вычислить, умножив площадь всего круга на отношение известного угла к 360 ° или 2π радианам, как показано в следующем уравнении:
| площадь = | × πr 2 | , если θ в градусах |
или
| площадь = | × πr 2 | , если θ в радианах |
Фермер и его дочь — разделение семьи
Фермер и его семья столкнулись с самой серьезной дилеммой на сегодняшний день.Прошел год, дочери фермера исполнилось 16 лет, и в рамках празднования ее дня рождения ее мать испекла ее любимый десерт — ежевичный пирог. К несчастью для дочери фермера, ежевичный пирог также является любимой едой их домашнего енота, Утконоса, о чем свидетельствует отсутствие пирога на 180 ° с явными признаками виновника в виде крошек, ведущих к чрезмерно увлеченному еноту. Изначально пирог легко можно было разделить между тремя людьми и одним енотом, но теперь половину пирога приходится делить между тремя людьми, поскольку огорченный, но пресыщенный Утконос наблюдает издали.Учитывая, что каждый человек получит пирог на 60 ° с радиусом 16 дюймов, площадь пирога, которую получает каждый человек, можно рассчитать следующим образом:
площадь = 60 ° / 360 ° × π × 16 2 = 134,041 дюйм 2
В результате невнимательности Утконоса каждый получает на треть меньше, и дочь задумчиво вспоминает урок американской истории, где она узнала о битве при Аламо и изображении народного героя Дэви Крокетта и его шляпы из енотовидной шкуры.
Эллипс
Эллипс — это обобщенная форма круга и кривая на плоскости, где сумма расстояний от любой точки кривой до каждой из двух ее фокальных точек постоянна, как показано на рисунке ниже, где P равно любая точка эллипса, а F 1 и F 2 — это два фокусировки.
Когда F 1 = F 2 , полученный эллипс представляет собой круг. Большая полуось эллипса, как показано на рисунке, который является частью калькулятора, является самым длинным радиусом эллипса, а малая полуось — самым коротким.Большая и малая оси относятся к диаметрам, а не радиусам эллипса. Уравнение для вычисления площади эллипса аналогично уравнению для вычисления площади круга, с той лишь разницей, что используются два радиуса, а не один (поскольку фокусы находятся в одном месте для круга):
area = πab
, где a и b — мажор
и малые полуоси
Фермер и его дочь — падение с орбиты
Прошло два года с момента загадочного исчезновения домашнего питомца, Утконоса, и случайного выигрыша пушистого аксессуара дочери фермера в школьной лотерее, который помогла заполнить пустоту потери их любимого питомца.Дочке фермера сейчас 18, и она готова сбежать из сельской Монтаны, чтобы жить в колледже, полной свободы и распутства, и, конечно же, немного поучиться на стороне. К несчастью для дочери фермера, она росла в среде, наполненной позитивным подкреплением, и, следовательно, с менталитетом, что нужно «стрелять на луну, [поскольку] даже если вы промахнетесь, вы приземлитесь среди звезд», а также утверждение всех окружающих, что она может делать абсолютно все, что захочет! Таким образом, с ее неоптимальными оценками, отсутствием какой-либо внеклассной деятельности из-за ее бесчисленного множества различных интересов, отнимающих все ее свободное время, нулевого планирования и ее настойчивого стремления поступать только в самые лучшие из лучших университетов, шок, который возник, когда она не была принята ни в один из ведущих университетов, в которые она подавала документы, можно было бы разумно сравнить с ее метафорической посадкой в глубоком космосе, надуванием, замерзанием и быстрым удушьем, когда она пропустила луну и приземлилась среди звезд.Наряду с легкими ее мечта стать астрофизиком была безнадежно разрушена, по крайней мере, на время, и ей пришлось вычислить эллиптическую площадь, необходимую в ее комнате, чтобы построить модель почти эллиптической орбиты Земли вокруг Солнца размером с человека. чтобы она могла с тоской смотреть на солнце в центре своей комнаты и его олицетворение ее сердца, пылающего страстью, но окруженного холодными просторами космоса, с далеким вращением Земли, насмешливо представляющим расстояние между ее мечтами и твердой землей .
площадь = π × 18 футов × 20 футов = 1130,97 кв. Футов
Параллелограмм
Параллелограмм — это простой четырехугольник, у которого есть две пары параллельных сторон, причем противоположные стороны и углы четырехугольника равны по длине и углам. Прямоугольники, ромбы и квадраты — это частные случаи параллелограммов. Помните, что классификация «простой» формы означает, что форма не является самопересекающейся. Параллелограмм можно разделить на прямоугольный треугольник и трапецию, которые в дальнейшем можно преобразовать в прямоугольник, что делает уравнение для вычисления площади параллелограмма по существу таким же, как и для вычисления прямоугольника.Однако вместо длины и ширины параллелограмм использует основание и высоту, где высота — это длина перпендикуляра между парой оснований. Основываясь на рисунке ниже, уравнение для вычисления площади параллелограмма выглядит следующим образом:
площадь = b × h
Фермер и его дочь — Алмаз в небе
Прошло еще два года в жизни фермера и его семьи, и, хотя его дочь вызывала сильное беспокойство, она наконец преодолела расстояние между пылающим солнцем, которое является ее сердцем, и Землей, на которой настаивает общество. она должна оставаться на земле.В результате борьбы, которая последовала за ее самоизоляцией, в окружении воображаемых, осуждающих глаз, предполагающих ее неудачу со всех сторон, дочь фермера вышла из-под натиска земли, как алмаз, ярко и твердо сияя в своей решимости. Несмотря на все его недостатки, она решает, что у нее нет другого выбора, кроме как оставаться в астероидном поле жизни в надежде, что финал сказки Диснея существует. Наконец-то, к счастью для дочери фермера и ее семьи, надежда появилась, но не в виде Прекрасного Принца, а скорее как знак с предполагаемых небес.Несмотря на все ее метафорические размышления и невзгоды, связанные с космосом, почти становится правдоподобным, что дочь фермера каким-то образом повлияла на массивный восьмигранный алмазный астероид, падающий прямо, но безопасно на их сельхозугодья, что она интерпретирует как представление ее путешествия, становления и возможного возвращения домой. Дочь фермера приступает к измерению площади одного из ромбовидных лиц своего недавно найденного символа жизни:
площадь = 20 футов × 18 футов = 360 квадратных футов
К несчастью для дочери фермера, появление огромного алмаза привлекло внимание со всего мира, и после достаточного давления она уступает человеку внутри себя и продает алмаз, само изображение ее жизни и души, какому-либо человеку. богатый коллекционер и продолжает жить остаток своей жизни в щедрых развлечениях, отказываясь от своих убеждений и теряясь в черной дыре общества.
Единицы общего пользования
| Единица | Площадь в м 2 |
| квадратных метров | SI Единица |
| га | 10,000 |
| квадратных километров (км 2 ) | |
| 1000 кв. фут | 0,0929 |
| квадратный ярд | 0,8361 |
| акров | 4,046,9 (43,560 квадратных футов) |
| квадратных миль | 2,589,988 (640 акров) |
Площадь поверхности конуса
Площадь поверхности куба
Площадь поверхности цилиндрического резервуара
Площадь прямоугольного резервуара
Площадь поверхности капсулы
Площадь поверхности крышки
Для расчета укажите любые два значения ниже.
Площадь поверхности конической усадки
Площадь поверхности эллипсоида
Площадь квадратной пирамиды
Калькулятор связанных объемов | Калькулятор площади | Калькулятор площади поверхности тела
Площадь поверхности твердого тела — это мера общей площади, занимаемой поверхностью объекта.Все объекты, рассматриваемые в этом калькуляторе, более подробно описаны на страницах «Калькулятор объема» и «Калькулятор площади». Таким образом, этот калькулятор будет сосредоточен на уравнениях для расчета площади поверхности объектов и использовании этих уравнений. Пожалуйста, обратитесь к вышеупомянутым калькуляторам для получения более подробной информации по каждому отдельному объекту.
Сфера
Площадь поверхности (SA) сферы можно рассчитать по формуле:
SA = 4πr 2
где r — радиус
Ксаэль не любит ни с кем делиться шоколадными трюфелями.Когда она получает коробку трюфелей Lindt, она приступает к вычислению площади поверхности каждого трюфеля, чтобы определить общую площадь поверхности, которую она должна лизать, чтобы уменьшить вероятность того, что кто-то попытается съесть ее трюфели. Учитывая, что каждый трюфель имеет радиус 0,325 дюйма:
SA = 4 × π × 0,325 2 = 1,327 дюйм 2
Конус
Площадь поверхности круглого конуса может быть вычислена путем суммирования площадей поверхности каждого из его отдельных компонентов.«Базовая SA» относится к кругу, который содержит основание в замкнутом круговом конусе, в то время как боковая SA относится к остальной части конуса между основанием и его вершиной. Уравнения для расчета каждого из них, а также общая SA замкнутого кругового конуса показаны ниже:
основание SA = πr 2
боковой SA = πr√r 2 + h 2
общая SA = πr (r + √r 2 + h 2 )
где r — радиус, а h — высота
Афина недавно проявила интерес к культуре Юго-Восточной Азии и особенно увлеклась конической шляпой, обычно называемой «рисовой шляпой», которая широко используется в ряде стран Юго-Восточной Азии.Она решает сшить свое собственное и, будучи очень практичным человеком, не погрязшим в сентиментальности, достает свадебное платье своей матери из темных уголков гардероба, в котором оно находится. Она определяет площадь поверхности материала, необходимого для создания шляпы, радиусом 1 фут и высотой 0,5 фута следующим образом:
боковая SA = π × 0,4√0,4 2 + 0,5 2 = 0,805 футов 2
Куб
Площадь поверхности куба может быть вычислена путем суммирования общих площадей его шести квадратных граней:
SA = 6a 2
где a — длина кромки
Энн хочет подарить своему младшему брату кубик Рубика на его день рождения, но знает, что у ее брата мало внимания и он легко расстраивается.Она заказывает кубик Рубика, у которого все грани черные, и должна платить за настройку в зависимости от площади поверхности куба с длиной ребра 4 дюйма.
SA = 6 × 4 2 = 96 дюймов 2
Цилиндрический бак
Площадь поверхности закрытого цилиндра может быть вычислена путем суммирования общих площадей его основания и боковой поверхности:
база SA = 2πr 2
боковой SA = 2πrh
общая SA = 2πr (r + h)
где r — радиус, а h — высота
У Джереми есть большой цилиндрический аквариум, в котором он купается, потому что он не любит душ или ванну.Ему любопытно, остывает ли его нагретая вода быстрее, чем в ванне, и ему нужно рассчитать площадь поверхности его цилиндрического резервуара высотой 5,5 футов и радиусом 3,5 футов.
всего SA = 2π × 3,5 (3,5 + 5,5) = 197,920 футов 2
Прямоугольный бак
Площадь прямоугольного резервуара равна сумме площадей каждой из его граней:
SA = 2lw + 2lh + 2wh
где l — длина, w — ширина и h — высота
Банан, старшая дочь в длинной череде фермеров, выращивающих бананы, хочет преподать своей испорченной гнилой младшей сестре Банановый хлеб урок о надеждах и ожиданиях.Banana-Bread всю неделю настаивает на том, чтобы ей нужен новый набор ящиков для размещения ее новых фигурок Бэтмена. Таким образом, Банана покупает ей большой кукольный домик Барби с кухонной утварью ограниченного выпуска, духовкой, фартуком и реалистичными гниющими бананами для Бэтмена. Она упаковывает их в прямоугольную коробку таких же размеров, как выдвижной ящик, который требуется Banana-Bread, и ей нужно определить количество оберточной бумаги, необходимое для завершения презентации подарка — сюрприза размером 3 фута × 4 фута × 5 футов:
SA = (2 × 3 × 4) + (2 × 4 × 5) + (2 × 3 × 5) = 94 футов 2
Капсула
Площадь поверхности капсулы может быть определена путем комбинирования уравнений площади поверхности для сферы и площади боковой поверхности цилиндра.Обратите внимание, что площадь поверхности оснований цилиндра не включена, поскольку она не составляет часть площади поверхности капсулы. Общая площадь рассчитывается следующим образом:
SA = 4πr 2 + 2πrh
где r — радиус, а h — высота
Горацио производит плацебо, которое призвано оттачивать индивидуальность человека, критическое мышление и способность объективно и логично подходить к различным ситуациям.Он уже протестировал рынок и обнаружил, что подавляющее большинство выборочной совокупности не проявляют ни одного из этих качеств и очень готовы купить его продукт, еще больше закрепившись в чертах, от которых они так отчаянно стремятся избавиться. Горацио должен определить площадь поверхности каждой капсулы, чтобы он мог покрыть их чрезмерным слоем сахара и обратиться к предрасположенным к сахару языкам населения при подготовке к следующему плацебо, которое «вылечит» все формы сахарного диабета.Учитывая, что каждая капсула имеет r 0,05 дюйма и h 0,5 дюйма:
SA = 4π × 0,05 2 + 2π × 0,05 × 0,5 = 0,188 дюйма 2
Сферический колпачок
Площадь поверхности сферического колпачка зависит от высоты рассматриваемого сегмента. Предоставленный калькулятор предполагает твердую сферу и включает основание крышки в расчет площади поверхности, где общая площадь поверхности является суммой площади основания и боковой поверхности сферической крышки.Если вы используете этот калькулятор для вычисления площади поверхности полой сферы, вычтите площадь поверхности основания. Учитывая два значения высоты, радиуса крышки или радиуса основания, третье значение можно вычислить с помощью уравнений, представленных в Калькуляторе объема. Уравнения площади поверхности следующие:
сферическая крышка SA = 2πRh
база SA = πr 2
Полная твердая сфера SA = 2πRh + πr 2
где R — радиус сферической крышки, r — радиус основания, а h — высота
Дженнифер завидует миру, который ее старший брат Лоуренс подарил на свой день рождения.Поскольку Дженнифер на две трети младше своего брата, она решает, что заслуживает одну треть земного шара своего брата. Вернув ручную пилу отца в сарай для инструментов, она вычисляет площадь поверхности своей полой части земного шара с R 0,80 футов и h 0,53 фута, как показано ниже:
SA = 2π × 0,80 × 0,53 = 2,664 фута 2
Коническая усадка
Площадь поверхности твердого прямоугольного усеченного конуса равна сумме площадей его двух круглых концов и площади его боковой поверхности:
круговой конец SA = π (R 2 + r 2 )
боковая SA = π (R + r) √ (R-r) 2 + h 2
всего SA = π (R 2 + r 2 ) + π (R + r) √ (R-r) 2 + h 2
где R и r — радиусы концов, h — высота
Пол делает вулкан в форме усеченного конуса для своего проекта научной ярмарки.Пол рассматривает извержения вулканов как явление насилия и, выступая против всех форм насилия, решает сделать свой вулкан в форме замкнутой конической усеченной пирамиды, которая не извергается. Хотя его вулкан вряд ли произведет впечатление на судей научной ярмарки, Пол все же должен определить площадь поверхности материала, который ему нужен для покрытия внешней стены своего вулкана с помощью R 1 фут, R 0,3 фута и h 1,5 фута:
всего SA = π (1 2 + 0,3 2 ) + π (1 + 0.3) √ (1 — 0,3) 2 + 1,5 2 = 10,185 футов 2
Эллипсоид
Для вычисления площади поверхности эллипсоида нет простой и точной формулы, такой как куб или другая более простая форма. В калькуляторе выше используется приблизительная формула, предполагающая, что эллипсоид почти сферический:
SA ≈ 4π 1,6 √ (a 1,6 b 1,6 + a 1,6 c 1,6 + b 1,6 c 1,6 ) / 3
где a , b и c — оси эллипса
Колтейн всегда любил готовить и недавно выиграл на конкурсе керамический нож.К несчастью для своей семьи, которая почти полностью ест мясо, Колтейн практиковал свою технику нарезки чрезмерного количества овощей. Вместо того, чтобы есть овощи, отец Колтейна уныло смотрит на свою тарелку и оценивает площадь поверхности эллиптических разрезов цуккини с осями 0,1, 0,2 и 0,35 дюйма:
SA ≈ 4π 1,6 √ (0,1 1,6 0,2 1,6 + 0,1 1,6 0,35 1,6 + 0,2 1,6 0,35 1.6 ) / 3 = 0,562 дюйма 2
Квадратная пирамида
Площадь поверхности квадратной пирамиды состоит из площади ее квадратного основания и площади каждой из четырех треугольных граней. Учитывая высоту h и длину кромки a , площадь поверхности можно рассчитать с помощью следующих уравнений:
база SA = 2
боковой SA = 2a√ (a / 2) 2 + h 2
всего SA = a 2 + 2a√ (a / 2) 2 + h 2
В классе Вонквайлы недавно завершено строительство модели Великой пирамиды в Гизе.Тем не менее, она считает, что модель не излучает того архитектурного чуда, как оригинал, и решает, что покрытие ее «снегом», по крайней мере, придаст вид чуда. Она вычисляет площадь поверхности расплавленного сахара, которая потребуется ей, чтобы полностью покрыть пирамиду, с длиной ребра на 3 фута и высотой h 5 футов:
всего SA = 3 2 + 2 × 3√ (3/2) 2 + 5 2 = 40,321 футов 2
В отличие от Великой пирамиды в Гизе, которая простояла тысячи лет, ее модель, сделанная из крекеров Грэма и покрытая сахаром, просуществовала всего несколько дней.
Единицы общего пользования
| Единица | метр 2 |
| километр 2 | 1,000,000 |
| сантиметр 2 | 0,0001 |
| микрометр | 0,000000000001 |
| га | 10,000 |
| миля 2 | 2,589,990 |
| ярд 2 | 0.83613 |
| фут 2 | 0,092903 |
| дюйм 2 | 0,00064516 |
| акров | 4,046,86 |
Калькулятор ромбов
Ромб в форме
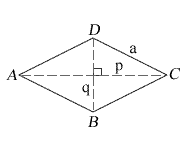
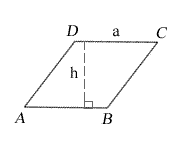
Эти два рисунка относятся к одному и тому же одинарному ромбу.
a = длина сторон
p = длинная диагональ
q = более короткая диагональ
h = высота
A, B, C, D = угловые уголки
K = площадь
P = периметр
π = пи = 3.1415926535898
√ = квадратный корень
Использование калькулятора
Вычислить некоторые переменные ромба в зависимости от предоставленных входных данных. Вычисления включают длину сторон, углы углов, диагонали, высоту, периметр и площадь ромба.
Ромб — это четырехугольник, противоположные стороны которого параллельны, а все стороны равны по длине. Ромб, у которого все углы прямые, называется площадь.Ромб (или ромб) — это параллелограмм со всеми 4 сторонами равной длины.
Единицы: Обратите внимание, что единицы длины показаны для удобства. Они не влияют на расчеты. Единицы измерения указывают порядок вычисленных результатов, например футы, футы 2 или футы 3 . Можно заменить любой другой базовый блок.
Формулы и ограничения ромба
Уголки: A, B, C, D
- А = С
- B = D
- A + B = 180 ° = π радиан
- для ромба, не являющегося квадратом,
- 0
- 90 °
- 0
Площадь: К
с A и B в радианах,
K = ah = a 2 sin (A) = a 2 sin (B) = pq / 2
Высота: h
- h = h a = h b
- h = грех (A) = грех (B)
Диагонали: p, q
- p = a √ (2 + 2 cos (A)) = a √ (2 — 2 cos (B))
- q = a √ (2-2 cos (A)) = a √ (2 + 2 cos (B))
- p 2 + q 2 = 4a 2
Периметр: P
P = 4a
Rhombus Вычислений:
Следующие формулы, основанные на приведенных выше, используются в этом калькуляторе для выбранных вариантов расчета.
- Вычислить B, C, D | Учитывая A
По заданному углу A вычислить углы B, C и D- В = 180 ° — А
- С = А
- D = B
- Вычислить A, C, D | Учитывая B
По заданному углу B вычислить углы A, C и D- А = 180 ° — В
- С = А
- D = B
- Рассчитать | Учитывая P
С учетом периметра вычислить сторону a - Рассчитать P | Учитывая
Заданная длина стороны a рассчитать периметр - Вычислить B, p, q, h, P, K | Учитывая a, A
По заданной длине стороны a и углу A вычислить диагонали, периметр, высоту, площадь и углы B, C и D- p = √ (2a 2 + 2a 2 cos (A))
- q = √ (2a 2 — 2a 2 cos (A))
- P = 4a
- h = грех (A)
- К = ах
- В = 180 ° — А
- С = А
- D = B
- Вычислить A, B, q, h, P, K | Учитывая а, р
По заданной длине стороны a и диагонали p вычислить диагональ q, периметр, высоту, площадь и углы A, B, C и D- A = arccos (1 — (p 2 /2 a 2 ))
- q = √ (2a 2 — 2a 2 cos (A))
- h = грех (A)
- P = 4a
- K = a 2 sin (A)
- В = 180 ° — А
- С = А
- D = B
- Вычислить A, B, p, h, P, K | Учитывая a, q
По заданной длине стороны и диагонали q вычислить диагональ p, периметр, высоту, площадь и углы A, B, C и D- A = arccos (1 + (q 2 / 2a 2 ))
- p = √ (2a 2 + 2a 2 cos (A))
- h = грех (A)
- P = 4a
- K = a 2 sin (A)
- В = 180 ° — А
- С = А
- D = B
- Вычислить A, B, p, q, P, K | Учитывая a, h
По заданной длине и высоте стороны вычислить диагонали, периметр, площадь и углы A, B, C и D- A = arcsin (ч / год)
- p = √ (2a 2 + 2a 2 cos (A))
- q = √ (2a 2 — 2a 2 cos (A))
- P = 4a
- K = a 2 sin (A)
- В = 180 ° — А
- С = А
- D = B
- Вычислить A, B, p, q, h, P | Учитывая a, K
По заданной длине стороны и площади вычислить диагонали, периметр, высоту и углы A, B, C и D- A = arcsin (K / a 2 )
- p = √ (2a 2 + 2a 2 cos (A))
- q = √ (2a 2 — 2a 2 cos (A))
- h = грех (A)
- P = 4a
- В = 180 ° — А
- С = А
- D = B
- Вычислить a, A, B, p, q, P | Учитывая К, ч
По заданной площади и высоте вычислить длину стороны, диагонали, периметр и углы A, B, C и D- a = К / ч
- P = 4a
- A = arcsin (K / a 2 )
- p = √ (2a 2 + 2a 2 cos (A))
- q = √ (2a 2 — 2a 2 cos (A))
- В = 180 ° — А
- С = А
- D = B
- Вычислить a, A, B, q, h, P | Учитывая K, p
По диагонали p и площади вычислите периметр, высоту, длину стороны, диагональ q и углы A, B, C и D- q = 2К / п
- a = √ (p 2 + q 2 ) / 2
- P = 4a
- A = arccos (1 — (p 2 /2 a 2 ))
- h = грех (A)
- В = 180 ° — А
- С = А
- D = B
- Вычислить a, A, B, p, h, P | Учитывая K, q
По диагонали q и площади вычислите периметр, высоту, длину стороны, диагональ p и углы A, B, C и D.- p = 2K / q
- a = √ (p 2 + q 2 ) / 2
- P = 4a
- A = arccos (1 + (q 2 / 2a 2 ))
- h = грех (A)
- В = 180 ° — А
- С = А
- D = B
- Вычислить a, B, p, q, P, K | Учитывая A, h
По заданному углу A и высоте вычислить сторону a, углы B, C и D, диагонали, периметр и площадь- a = h / sin (A)
- P = 4a
- p = √ (2a 2 + 2a 2 cos (A))
- q = √ (2a 2 — 2a 2 cos (A))
- K = a 2 sin (A)
- В = 180 ° — А
- С = А
- D = B
- Вычислить a, A, B, h, P, K | Учитывая p, q
По диагонали p и диагонали q вычислить длину стороны, углы A, B, C и D, высоту, периметр и площадь.- a = √ (p 2 + q 2 ) / 2
- P = 4a
- К = (p * q) / 2
- A = arcsin (K / a 2 )
- В = 180 ° — А
- С = А
- D = B
- h = грех (A)
Ссылки
Цвиллинджер, Даниэль (главный редактор). Стандартные математические таблицы и формулы CRC, 31-е издание New York, NY: CRC Press, p. 323, 2003.
Математический форум: Спросите доктора математики FAQ: Четырехугольные формулы (http://mathforum.org/)
Вайсштейн, Эрик У. «Ромб». От MathWorld — Интернет-ресурс Wolfram. Ромб.
.
